高中数学:各大题型详细方法解题方法总结,高考生一定要看
高考数学大题考查的包括三角函数、立体几何、数列、圆锥曲线、函数与导数。
每类题都有对应的出题套路,每一种套路都有对应的解题方法:
三角函数
三角函数的题有两种考法,其中10%~20%的概率考解三角形,80%~90%的概率考三角函数本身。
高考考查:三角函数与解三角形结合,高考会考一个大题,难度一般不会太大,属于不能丢分的板块。
同时后面立体几何、圆锥曲线与导数的学习,也需要用到三角函数作为辅助工具。所以,这块内容要引起重视学扎实来,不能掉以轻心。
1.解三角形
不管题目是什么,要明白,关于解三角形,只学了三个公式一一正弦定理、余弦定理和面积公式。
所以,解三角形的题目,求面积的话肯定用面积公式。至于什么时候用正弦,什么时候用余弦,如果你不能迅速判断,都尝试一下也未尝不可。
2.三角函数
然后求解需要求的。套路一般是给一个比较复杂
的式子,然后问这个函数的定义域、值域、周期、频率、单调性等问题。
解决方法就是,首先利用“和差倍半”对式子进行化简。化简成:

掌握以上公式足够了,关于题型见下图:

立体几何
立体几何在高考中非常重要。
立体几何在高考中一般会有一道大题和一道小题,分值在17-22分左右,2020年高考最高考了27分。
立体几何太难?感觉好抽象怎么突破
很多高一的同学都说立体几何太难了,尤其是很多女生觉得太抽象了,不知道怎么去处理各种线和面的关系。
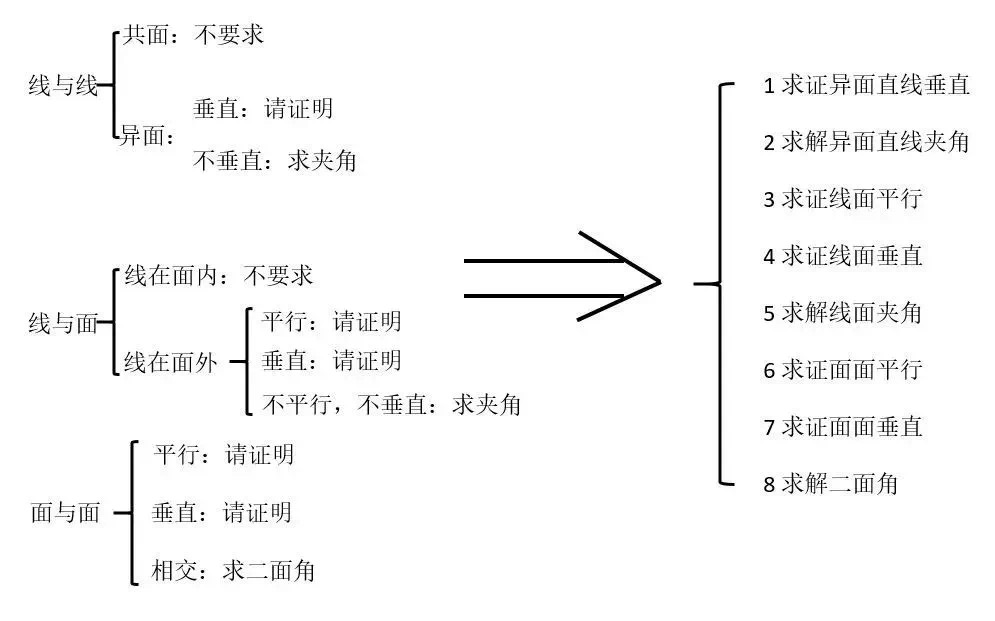
很多同学难以突破立体几何,其中一个重要原因就是,记住了很多定理和性质,但是没有真正弄懂它们的本质,只是机械的记住了而已。比如说,证明线面垂直,需要证明这条直线与平面内的两条相交直线分别垂直,很多同学可能会做;但一遇到证明线线垂直就不会了,最简单就是能直接证明或者通过平移证明,但是证明线线垂直的考法,不会这么单纯简单,一般都是要通过线面垂直,再推到线线垂直。
所以,证线线垂直的核心依然是线线垂直,只不过多了一步,由线面垂直推到线线垂直而已,真正搞懂了并不难。但很多同学没有去总结和思考性质和定理的本质,所以感觉很难。至于线面角和二面角不会找角,也是同样的道理。
立体几何的相关题目,稍微复杂一些,可能会卡住一些人。
这个题目一般有2~3问,一般会考查某条线的大小或者证明某个线/面与另外一个线/面平行或垂直,以及求二面角。